Square Packing
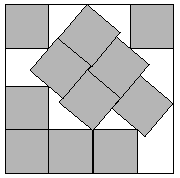
The question here is: What is the smallest square that one can fit n unit squares in?
The problem is unsolved for n higher than 11, n not a square.
While bounds have been found, little progress has been made. This problem resembles Thomas Hales' work on the Kepler conjecture, though in one less dimension. Simple code can be written to establish bounds, simply by randomly assorting squares. An interesting research question would involve characterizing "minimal patterns", in such a way that composite n can be broken down into components.
The problem is unsolved for n higher than 11, n not a square.
While bounds have been found, little progress has been made. This problem resembles Thomas Hales' work on the Kepler conjecture, though in one less dimension. Simple code can be written to establish bounds, simply by randomly assorting squares. An interesting research question would involve characterizing "minimal patterns", in such a way that composite n can be broken down into components.
